Intrinsic Dimensions (the TwoNN perspective)
This post is going to talk about the concepts of Intrinsic dimensions (i.e., roughly the minimum number of dimensions required to represent a piece of information). When we came across the idea of intrinsic dimensions, we were intrigued by the idea of computing the minimum number of dimensions required to explain a dataset. And interestingly, we found that the estimated intrinsic dimensions of the widely known MNIST dataset (computed by this method) is around ~14.something, making us think that the proposed ID estimation method is doing an incredible job in quantifying the information since the underlying information in MNIST is 10 (considering information present in the dataset in the form of digits) + some additional information present to vary the writing style of digits (~4.something) which decides the irregularities or variations present in the handwriting. However, it turns out that we were thinking in the wrong direction (as we will figure out later in the post).
This post is an attempt to understand and summarize the idea of intrinsic dimensions and their computation. Majorly this post tries to summarize the paper Facco et al., 2017 (generally referred to as TwoNN method of computing Intrinsic dimensions) relating the general idea of intrinsic dimension and its computation/estimation using Poisson point processes.
Outline
- Motivation
- Background
- Intrinsic Dimensions from TwoNN perspective
- Computing Intrinsic Dimensions
- Experiments
- Additional Experiments
- Sneak Peak to GRIDE
- Conclusion
- Further Readings
Motivation
Dimensionality reduction has always been an intriguing concept for computer scientists, with formalizations seen from Information Theory to Machine Learning. The primary idea being
- the maximum amount of compression that can be done
- or in other ways, how much information is in the data
- or, more formally, what are the minimum number of dimensions/variables in which the data can be explained (or nearly explained)?
Machine learning makes it even more interesting by establishing the famous manifold hypothesis and working towards manifold learning to dimensionality reductions (PCA, LDA/NDA, tSNE, and other Nonlinear dimensionality reduction methods). Some of the popular topics include the exciting idea behind Eigen Faces. Additionally, there has been an intensive set of works targetting the low-dimensional feature space in deep neural networks. However, the primary question still roots down to the presence of intrinsic dimensions in a dataset and how to compute them.
The concept of intrinsic dimensions and their applications seems intuitive and exciting, but how can we compute/estimate (or approximate 🤔) the intrinsic dimensions of a dataset whose dimensions appear to be humongous (like in HD images)? In this post, we would like to work with the underlying math behind making such approximations. We will start by defining the necessary mathematical background and build towards the methods proposed by Facco et al., 2017.
Background
The one and only concept that we would need for this post is the Poisson process. In simple terms, the Poisson process or Poisson point process helps model the independent occurrence of points located in a space. For example, it can be a representation of buses arriving at a bus stop where the points are distributed in time or a representation of RADAR detections where the airplanes are scattered in space or meeting new people in an event where the points are distributed in both space and time.
$$ \text{The Poisson Distribution} $$
A discrete random variable follows Poission distribution with parameter $\lambda$ and the probability mass function is given by
$$ \begin{aligned} \displaystyle \mathrm{Poisson}(k; \lambda) = \dfrac{\lambda^k e^{-\lambda}}{k!} \qquad \text{for } k \in \mathbb{N}, \lambda > 0 \end{aligned} $$
It gives the probability of observing $k$ events in a fixed time interval given that the events occur independently at a constant rate $\lambda$. $\newline$
Hypothetically, if you are a lone wanderer 🗺️ and have a long layover in an airport and are waiting for your flight details in front of the dashboard and are also interested in the number of airplanes that arrive 🛬 at the airport during a specific time period ⏱️, such as one hour. Then, Poisson distribution is the thing that you should look at. Poisson distribution helps answer the question, “What is the probability that $k$ airplanes have arrived in a given hour?”.
$$ \text{The Poisson Process} $$
Let $\lambda >0$ be fixed, The counting process $\{N(t), t\in[0, \infin)\}$ is called a Poisson process with rates $\lambda$ if all the following conditions hold:
- $N(0)=0$
- $N(t)$ has independent increments
- The number of arrivals in any interval of lengths $\tau>0$ has $\mathrm{Poisson}(\lambda \tau)$ distribution.
The Poisson process extends Poisson distribution to a continuous time domain. It is a stochastic process that counts the number of events in a time interval. The time interval can be of any length, but it is assumed that the number of events occurring is proportional to the length of the time interval. So, in the Airport Layover scenario, the number of Airplanes arriving in a specific time period is proportional to the length of the time period.
$$ \text{Transformation of Random Variables} $$
Please feel free to skip this section if you are already familiar with the concept of transformation of random variables. This section is a quick recap of the concept and was added in the later version of the post to make it self-contained. Familiarity with the concept of transformation of random variables will help play around with the equations while building towards the idea presented in the TwoNN method of computing Intrinsic Dimensions.
The concept of transforming random variables involves creating a new random variable through a combination of existing ones. Broadly speaking, this process allows for a shift in perspective on the original random variable, offering a fresh understanding of its impact on a newly formed random variable. It is assumed that the transformation applied to the random variable is both differentiable and invertible across the entire range of values within the domain of the original random variable. The probability density function (PDF) of the transformed random variable can be calculated utilizing the following formulation:
$$ p(y) = p_x(U^{-1}(y)) \det\bigg|\bigg(\frac{\partial}{\partial y}U^{-1}(y)\bigg)\bigg| $$ where $U$ is the transformation function, and $p_x$ is the probability density of the random variable $X$.
We can visualize this for a two-dimensional random variable. Let $(U, V)$ be the two-dimensional random variable. We apply $f$ as a transformation such that $f(U, V) = (X, Y)$. The diagram below provides the probability density for $(U, V)$ (shown on the left) and the probability density for $(X, Y)$ (shown on the right).
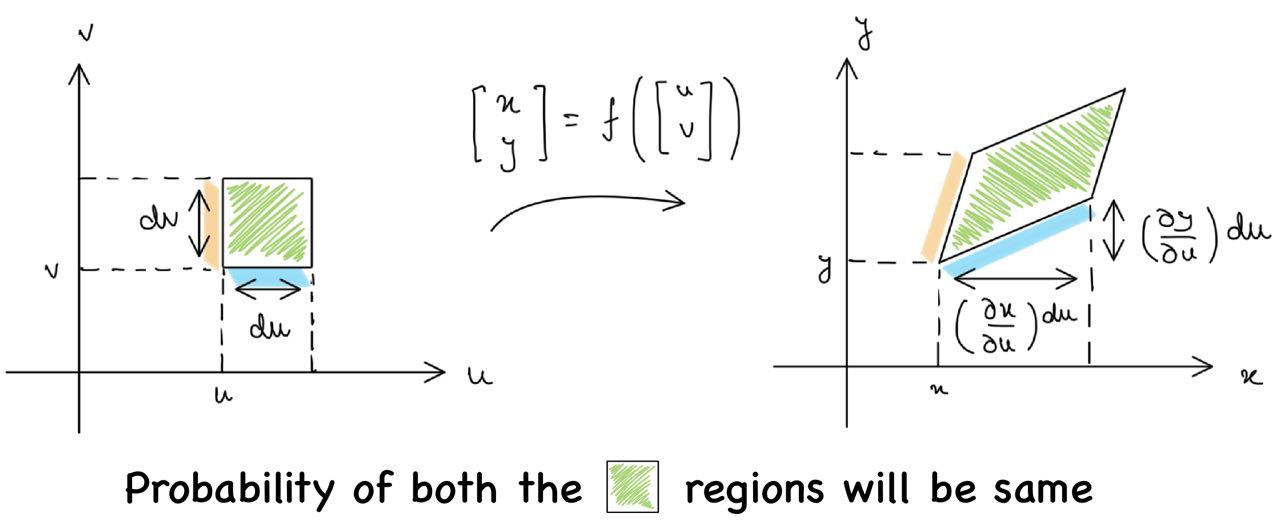
As the probability is the same, the area multiplied by the functional value will be the same. The magnitude of the cross product of adjacent sides gives the area enclosed by a parallelogram. Thus, we can write
$$ p_{UV}(u,v) du dv = p_{XY}(x,y) \begin{vmatrix} {\partial x \over \partial u}du & {\partial y \over \partial u}du \\ \\ {\partial x \over \partial v}dv & {\partial y \over \partial v} dv\end{vmatrix} $$
Manipulating the above equation, we get the following equation
$$ f_{UV}(u,v) = f_{XY}(x,y) \left|\partial (x,y) \over \partial (u,v)\right| $$
where the Jacobian determinant is the determinant of the Jacobian matrix of the transformation. It’s noteworthy that this expression holds true for any type of transformation, extending its applicability seamlessly to higher dimensions.
Intrinsic Dimensions from TwoNN perspective
Now, we are all set to proceed forward with the idea of computing intrinsic dimensions (primarily from the perspective of TwoNN). TwoNN takes the direction of a generative model and considers the data points to be generated from a Poisson process. Note that we are interested in computing the intrinsic dimensions of a given dataset (or a set of data points from a dataset). Suppose all the data points are part of a generative process modeled using a Poisson process in the low dimensional latent space. In that case, TwoNN shows that the intrinsic dimensions of the dataset can be computed just by considering the space/distance between the two nearest points, hence the name TwoNN.
Let’s consider $\Phi$ to be such a homogeneous Poisson process in $\R^d$ with density $\lambda$ that satisfies the following properties:
- For any disjoint Borel sets, $A_1$ and $A_2$, the random variable $N(A_1)$ and $N(A_2)$, describing the number of points falling in $A_1$ and $A_2$, respectively, are independent.
- The number of points $N(A)$ are distributed as a Poisson variable with parameter $\lambda \mu(A)$ where $\mu(A)$ is the measure of $A$ (like the area of $A$) $$ P(A \text{ contains exactly n points}) = P(N(A)=n) = {\frac{(\lambda \mu(A))^n}{n!}}e^{-\lambda \mu (A)} $$
- $P(N(A)= 0 ) = e^{-\lambda \mu(A)}$, i.e. the probability of having no points in a Borel set $A$
Facco et al., 2017 provide a pleasant and straightforward description in the supplementary material. Please feel free to refer to the supplemental material for more details.
Let’s try to see it from the perspective of a single data point present in space. Considering the center $o$ and the distance from the first nearest point as $r_1$, we can define a sphere $B_{o,r_1}$ with no data points. The probability of finding a point in this sphere is given by $$P(N(B_{o,r_1})=0) = e^{-\lambda \mu(B_{o,r_1})}$$
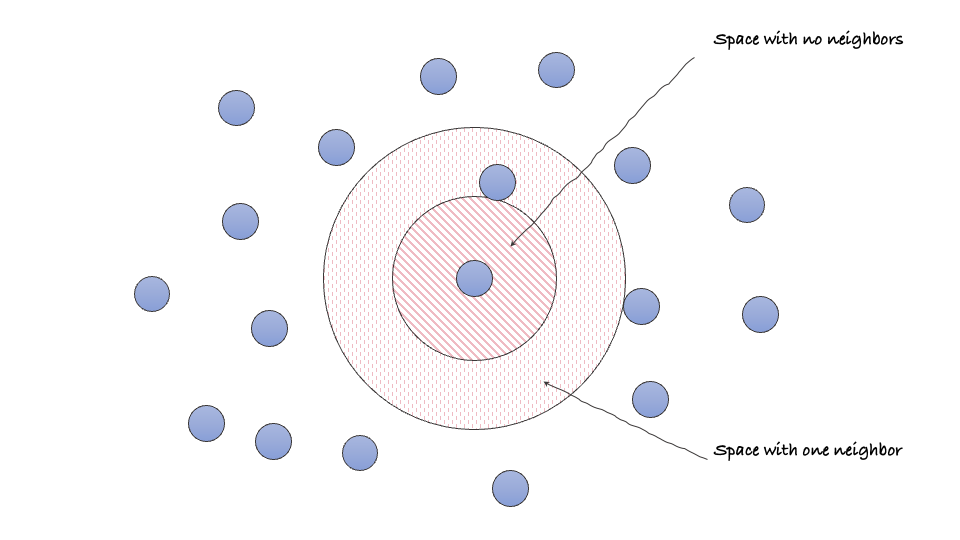
Extending the idea, we can also define an annulus $C_{r_1,r_2}$ with inner radius $r_1$ and outer radius $r_2$ where $r_2$ is the distance of the second nearest point from the reference point $o$. The probability of finding a point in this annulus is given by
$$P(N(C_{r_1,r_2})=0) = e^{-\lambda \mu(C_{r_1,r_2})}$$
Similarly, with the help of a reference data point $o$, we can order all the remaining data points according to the distance from our reference point. Let the distances for the ordered nearest points be $r_1, r_2, \ldots, r_n$ from the reference point $o$ ($r_0$ to be the distance from the reference point to itself, which will always be zero). We can now define $\Delta v_i $ as the volume of the annulus $C_{r_1,r_2}$ i.e. region between two concentric circles as
$$ \Delta v_i = w_d \left(r_i^d-r_{i-1}^d\right) $$
where $w_d$ is the volume of the $d$ dimensional sphere with unity radius. Further, we can extend this formulation for all the available data points by defining a function $U: \R^{n} \to \R^n$ as
$$ \Delta \vec v = U(\vec r)\\ \Rightarrow \Delta \vec v = w_d\begin{bmatrix} r_1^d - r_0^d \\ \vdots \\ r_n^d - r_{n-1}^d\end{bmatrix} $$
Remember, all we are interested in is the expression of the probability distribution of $\Delta \vec v$. As the relation between $\vec r$ and $\Delta \vec v$ has been established, we can bottleneck our way to find $p(\Delta \vec v)$ through the probability distribution $p(\vec r)$. We can utilize the sorted distances of other points $\left(r_1,r_2\cdots r_n \right)$ to move towards computing the joint probablity distribution $p(r_1,\cdots, r_n)$.
Looking from the perspective of a single data point $o$, and a list of remaining data points sorted in increasing order of distance from the reference point $o$, i,e. $\left(r_1,r_2\cdots r_n \right)$, we can start by computing the probability that the first distance $r_1$ falls in an infinitesimally small annulus $C_{r_1,r_1+\partial r_1}$, leading us to $P(r_1)$. Further, we can compute the probability that the second distance $r_2$ falls in an infinitesimally small annulus $C_{r_2,r_2+\partial r_2}$ given that the first distance $r_1$ falls in $C_{r_1,r_1+\partial r_1}$, leading us to the conditional probability $P(r_2\mid r_1)$. Further, applying the chain rule of probability, we can compute the joint probability $P(r_1,r_2)$ as $P(r_2\mid r_1)P(r_1)$. Finally, we can continue this process and find the entire joint distribution by considering all the distances $\left(r_1,r_2\cdots r_n \right)$.
Let’s start by finding the probability that the first distance $d_1$ falls in an infinitesimally small annulus $C_{r_1,r_1+\partial r_1}$, which is equal to the probability that no point falls in the sphere $B_{o,r_1}$, and there exists at least one point in the space $C_{r_1,r_1+\partial r_1}$
$$ \begin{aligned} P\left(d_1 \in C_{r_1, r_1+\partial r_1}\right) &=P\left(N\left(B_{o, r_1}\right)=0, N\left(C_{r_1, r_1+\partial r_1}\right) \geq 1\right) \\ &=P\left(N\left(B_{o, r_1}\right)=0\right) P\left(N\left(C_{r_1, r_1+\partial r_1}\right) \geq 1\right) \\ &={P\left(N\left(B_{o, r_1}\right)=0\right)} {\left(1-P\left(N\left(C_{r_1, r_1+\partial r_1}\right)=0\right)\right)} \\ &= e^{-\lambda \mu(B_{o,r_1})} \left(1 - e^{-\lambda \mu(C_{r_1, r_1+\partial r_1})}\right)\\ &= e^{-\lambda w_dr_1^d}\left(1-e^{-\lambda w_d((r_1 + \partial r_1)^d - r_1^d)}\right)\\ &= e^{-\lambda w_dr_1^d}\left(1-e^{-\lambda w_dr_1^d\left(\left(1 + {\partial r_1\over r_1}\right)^d - 1\right)}\right)\\ &= e^{-\lambda w_dr_1^d}\left(1-e^{-\lambda w_dr_1^d\left(1 + d{\partial r_1\over r_1} - 1\right)}\right)\\ &= e^{-\lambda w_dr_1^d}\left(1-e^{-\lambda dw_d r_1^{d-1}\partial r_1}\right)\\ &= e^{-\lambda w_dr^d_1} \lambda dw_dr^{d-1}_1\partial r_1 \end{aligned} $$
As a second step, we need the probability that $d_2$ will fall in $C_{r_2, r_2+\partial r_2}$ given that $d_1$ falls in $C_{r_1, r_1+\partial r_1}$
$$ \begin{aligned} P\left(r_2\mid r_1\right) &= P\left(d_2 \in C_{r_2, r_2+\partial r_2} \mid d_1 \in C_{r_1, r_1+\partial r_1}\right)\\ &= P\left(N\left(C_{r_1, r_2}\right)=0, N\left(C_{r_2, r_2+\partial r_2}\right) \geq 1\mid N\left(B_{o, r_1}\right)=0, N\left(C_{r_1, r_1+\partial r_1}\right) \geq 1\right)\\ &= P\left(N\left(C_{r_1, r_2}\right)=0, N\left(C_{r_2, r_2+\partial r_2}\right) \geq 1\right)\\ &= {P\left(N\left(C_{r_1, r_2}\right)=0\right)} {\left(1-P\left(N\left(C_{r_2, r_2+\partial r_2}\right)=0\right)\right)} \\ &= e^{-\lambda w_d\left({r^d_2 - r_1^d}\right)} \lambda dw_dr^{d-1}_2\partial r_2 \\ \\ P(r_1,r_2) &= P(r_2\mid r_1)P(r_1)\\ &= \left(e^{-\lambda w_d\left({r^d_2 - r_1^d}\right)} \lambda dw_dr^{d-1}_2\partial r_2\right)\left(e^{-\lambda w_dr^d_1} \lambda dw_dr^{d-1}_1\partial r_1\right)\\ &= e^{-\lambda w_d r_2^d}(\lambda d w_d)^2 (r_1r_2)^{d-1}\partial r_1\partial r_2 \end{aligned} $$
We can continue the above process and find the joint distribution as
$$ P(r_1,r_2,\dots, r_n) = e^{-\lambda w_d r_n^d} (\lambda d w_d)^n (r_1r_2\dots r_n)^{d-1} \partial r_1\partial r_2\dots \partial r_n $$
For the probability density function, we divide the above probability by $\partial r_1\partial r_2\dots \partial r_n$
$$ p(\vec r) = e^{-\lambda w_d r_n^d} (\lambda d w_d)^n (r_1r_2\dots r_n)^{d-1} $$
As we have computed $p(\vec r)$, we can apply the transformation of random variables defined above to get $p(\Delta \vec v)$. It can be computed as $$ p(\Delta \vec v) = p_{\vec r}(U^{-1}(\Delta \vec v)) \det\bigg|\bigg(\frac{\partial}{\partial \Delta \vec v}U^{-1}(\Delta \vec v)\bigg)\bigg| \\ $$
Solving for the first term
$$ \begin{aligned} &U(\vec r) = {\Delta \vec v}\\ \Rightarrow &\vec r = U^{-1}(\Delta \vec v)\\ \end{aligned} $$ $$ \begin{aligned} \Rightarrow &U^{-1}(\Delta \vec v) = {1\over w_d}\begin{bmatrix}{ (\Delta v_1)^{1\over d}}\\ (\Delta v_1 +\Delta v_2)^{1\over d}\\ \vdots\\ (\Delta v_1+\Delta v_2\cdots +\Delta v_n)^{1\over d}\end{bmatrix} \end{aligned} $$
$$ \Rightarrow p_r(U^{-1}(\Delta \vec v)) = \exp\left({-\lambda w_d\left({\left({\Delta v_1 +\dots + \Delta v_n \over w_d}\right)^{{1\over d}d}}\right)}\right) (\lambda d w_d)^n\\ \qquad \qquad \qquad \times\left({{(\Delta v_1)(\Delta v_1 + \Delta v_2)\dots (\Delta v_1 + \dots + (\Delta v_n))}^{1\over d}}\right)^{d-1}\\ $$
$$ \Rightarrow p_r(U^{-1}(\Delta \vec v)) = \exp\left({-\lambda\sum_{k=1}^{n} \Delta v_k}\right) (\lambda d w_d)^n \left(\prod_{k=1}^n\sum_{l=1}^i \Delta v_l \right)^{d-1 \over d} $$
Solving for the second term
$$ \Rightarrow{\partial U^{-1}(\Delta \vec v)\over \partial \Delta \vec v}\bigg|_{i,j} = {1\over w_d}{\partial {\left({{\Delta v_1+\cdots + \Delta v_i}}\right)}^{1\over d}\over \partial \Delta v_j} $$
note that for $j>i$ the $(i,j)$ entry of the jacobian matrix ${\partial U^{-1}(\Delta \vec v)\over \partial \Delta \vec v}$ will be $0$ as ${\left({{\Delta v_1+\cdots + \Delta v_i}}\right)}^{1\over d}$ is independent of $\Delta v_j$, resulting in a lower triangular matrix. As the determinant of a lower triangular matrix is the product of the diagonal entries, we only need to compute the diagonal elements of the Jacobian matrix to find the determinant.
For every $(i, i)$ entry in the matrix
$$ \begin{aligned} {\partial U^{-1} (\Delta v)\over \partial\Delta v} \bigg|_{(i,i)} &= {1\over w_d} {\partial {\left({{\Delta v_1+\cdots + \Delta v_i}}\right)}^{1\over d}\over \partial \Delta v_i}\\ &= {1\over dw_d}(\Delta v_1+\cdots + \Delta v_i)^{{1-d\over d}} \\ &= {1\over dw_d} \left(\sum _{l=1}^i \Delta v_l \right)^{{1-d\over d}} \end{aligned} $$
$$ \begin{aligned}\det\bigg|\bigg({\partial U^{-1}(\Delta v)\over \partial \Delta v}\bigg)\bigg| &= \prod_{k=1}^n {1\over dw_d} \left(\sum_{l=1}^i \Delta v_l\right)^{{1-d\over d}}\\ &= {1\over (dw_d)^n} \left(\prod_{k=1}^n\sum_{l=1}^i \Delta v_l\right)^{{1-d\over d}} \end{aligned} $$
Multiplying the two terms, we get
$$ \begin{aligned} p(\Delta \vec v) &= \lambda^n\exp\left({-\lambda\sum_{k=1}^{n} \Delta v_k}\right) \end{aligned} $$
As each $\Delta v_i$ is independent of each other, we can write the above equation as $$ \begin{aligned} % p(\Delta \vec v) &= \lambda^n\exp\left({-\lambda\sum_{k=1}^{n} \Delta v_k}\right)\\ \prod_{k=1}^n p(\Delta v_k)&= \prod_{k=1}^n\lambda\exp\left({-\lambda\Delta v_k}\right)\\ \end{aligned} $$
$$ p(\Delta v_i) = \lambda e^{-\lambda \Delta v_i}\\ \Rightarrow P(\Delta v\in [v,v+dv]) = \lambda e^{-\lambda v}\partial v $$
The probability of finding a particle in a volume $dv$ is the exponential distribution. Note that we are still unaware of the $\lambda$ term here. Hence, we need modify the obtained equation in a manner where the dependency over the unknown $\lambda$ is removed. We can consider taking the ratio of the $i^{th}$ and the $j^{th}$ element of $\Delta \vec v$ to remove the dependency over $\lambda$. Hence, a new term $R$, is defined as the ratio of the two volumes $v_j$ and $v_i$.
$$ R = {\Delta v_i \over \Delta v_j} $$
Further, finding the probability density function for $R$ $$ \begin{aligned} P(R\in [\overline{R},\overline{R} + \partial \overline{R}])&= \int_0^\infin \partial v_i \int_0^\infin \partial v_j \lambda^2e^{-p(v_i+v_j)} \mathcal{I}\left\{ {v_j\over v_i}\in [\overline{R},\overline{R} + d\overline{R}]\right\}\\ &= \int_0^\infin \partial v_i \int_{\overline{R}}^{\overline{R} + \partial \overline{R}} \partial v_j \lambda^2e^{-\lambda(v_i+v_j)} \\ &= \lambda^2\int_0^\infin e^{-\lambda v_i}\partial v_i \int_{\overline{R}}^{\overline{R} + \partial \overline{R}} e^{-\lambda v_j}\partial v_j \\ &= \lambda\int_0^\infin e^{-\lambda v_i}\partial v_i \left[e^{-\lambda\overline{R}v_i} - e^{-\lambda(\overline{R} + \partial\overline{R})v_i}\right] \\ &= \lambda\int_0^\infin e^{-\lambda v_i}\partial v_i e^{-\lambda\overline{R}v_i}\left[1 - e^{-\lambda \partial\overline{R}v_i}\right] \\ &= \lambda\int_0^\infin e^{-\lambda v_i}dv_i e^{-\lambda\overline{R}v_i}\left[1 - 1 + \lambda \partial Rv_i\right] \\ &= \lambda^2 \partial R\int_0^\infin v_ie^{-\lambda v_i(1+\overline{R})}\partial v_i \\ &= \lambda^2\partial R \left(-{(\lambda(\overline{R}+1)v_i +1) e^{-\lambda\overline{R}v_i-\lambda v_i}\over \lambda^2(1+\overline{R})^2}\right)\bigg|_{0}^\infin \\ &= {\partial R\over (1+R)^2} \end{aligned} $$
Hence, the probability density function for $R$ is given by $$ p(R) = {1\over (1+R)^2} $$
However, the distribution obtained above does not depend on the dimension of the space. We can further massage through the above formulation to find the probability density function for the ratio of the two nearest neighbors $\mu = {r_2 \over r_1}$, helping to include the dependency over the dimension of the space.
$$ R = {r_2^d -r_1^d \over r_1^d - r_0^d} = {r_2^d - r_1^d\over r_1^d} = \mu^d - 1\\ \Rightarrow \mu = (1+R)^{1\over d} $$
We can again apply the transformation of random variables and get the probability density function for $\mu$
$$ p(R) = {1\over (1+R)^2}\\ F_{\mu}(\mu_0) = \begin{cases} P\{\mu \le \mu_0\} & \mu_0 \ge 1 \\ 0 & \mu_0 < 1\end{cases} $$
$$ \begin{aligned} F_\mu (\mu_0) &= P\{\mu \le \mu_0\} \mathcal I\{\mu_0 \in [1,\infin)\} \\ &= P\{(1+R)^{1\over d} \le \mu_0\} \mathcal I\{\mu_0 \in [1,\infin)\} \\ &= P\{R \le \mu_0^d - 1\} \mathcal I\{\mu_0 \in [1,\infin)\} \\ &= \left(\int_0^{\mu_0^d -1} {1\over (1+R)^2} dR\right)\mathcal I\{\mu_0 \in [1,\infin)\} \\ &= -{1\over 1+R} \bigg|_0^{\mu_0^d-1}\mathcal I\{\mu_0 \in [1,\infin)\} \\ &= (1-\mu_0^{-d})\mathcal I\{\mu_0 \in [1,\infin)\} \end{aligned} $$
differentiating the above equation, we get the probability density function for $\mu$ $$ \begin{aligned} p_\mu(\mu_0) &= {d\over d\mu_0}F_\mu(\mu_0) \\ &= \frac{d}{\mu_0^{d+1}} \mathcal I\{\mu \in [1,\infin)\} \end{aligned} $$
The obtained probability density function for $\mu$ is a standard probability distribution, i.e., Pareto distribution with parameters $1$ and $d$. $$ \implies \mu \sim \mathrm{Pareto}(1,d) $$
Notice that for a given dataset, we can empirically approximate the cumulative distribution function $F(\mu)$ by taking the ratio of the number of points with $\mu \le \mu_0$ to the total number of points in the dataset. (see Kolmogorov–Smirnov test)
From the above equation of $F(\mu)$, we can rearrange the terms to get $d$ as a function of $\mu$ and $F(\mu)$
$$ \begin{gathered} F(\mu)=\left(1-\mu^{-d}\right) \mathcal I_{[1,+\infty]}(\mu) \\ -\frac{\log (1-F(\mu))}{\log (\mu)}=d \end{gathered} $$
Thus, we can show the formulation for the intrinsic dimension as a function of $\mu$ and $F(\mu)$, where both $\mu$ and $F(\mu)$ are empirically computable from the dataset.
Computing Intrinsic Dimensions
After massaging through the equations, the computation of intrinsic dimensions boils down to a simple formulation. $$ d = -\frac{\log (1-F(\mu))}{\log (\mu)} $$
where $\displaystyle \mu = {r_2\over r_1}$.
For computing intrinsic dimensions of the given data points $D_i\{i=1,2,\ldots, N \}$, we can start with computing the pairwise distances for each datapoint and finding the two shortest distances $r_1$ and $r_2$, hence computing $\mu_i \{i=1,2,\ldots, N\}$. As $F(\mu)$ is the cumulative distribution (cdf) obtained by integration, for a dataset, we can empirically compute it by taking $$ \displaystyle F^{emp}(\mu) \dot{=} {i\over N} $$
Now we have both two sets of points for our dataset $\log(1-F(\mu))$ and $\log({\mu})$, and as the ratio or slope of the two gives us the dimension $d$, we can fit a linear regressor passing through origin over these points to approximate the slope. Bac et al., 2021 provide a nice implementation of the TwoNN algorithm here in scikit-dimension.
Notice that though we assumed the generative poission process to be in $\mathbb{R}^d$ (intrinsic dimension space), we are computing the intrinsic dimensions using the approximations of the data points in the original space (value of $\mu, F(\mu)$ approximated using distance between the actual data points).
Since the manifold hypothesis assumes the underlying data points to lie in a low dimensional manifold, we can consider the data points to be mapped to a lower dimensional manifold where the local neighborhood is preserved as in the original space, i.e., the points that are close in the lower dimensional manifold are also close in the original space. Hence, we can assume the ratio of the two nearest neighbors in the original space to be the same as the ratio of the two nearest neighbors in the intrinsic dimension space, making it a good approximation for the intrinsic dimension.
Experiments
Toy Datasets
Scikit-dimension also provides a set of toy datasets to play around with. For validating the TwoNN algorithm over a range of intrinsic dimensions, we consider all the datasets available in the library and compute the intrinsic dimensions for each using the TwoNN algorithm. The Figure below highlights the predicted intrinsic dimensions along with the actual intrinsic dimensions. The red line represents the expected prediction over the range of intrinsic dimensions.
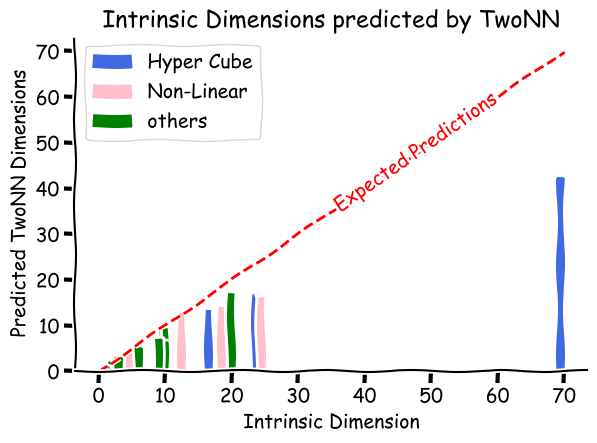
We observe that though TwoNN can predict the intrinsic dimensions of the toy datasets with lower intrinsic dimensions, it fails to predict the intrinsic dimensions as the number of intrinsic dimensions increases, making the predictions far from true intrinsic dimensions. This is because the ratio of the two nearest neighbors $\mu$ becomes more concentrated around $1$ as the dimension increases, highlighting the direct implications of the curse of dimensionality. The paper provides a more detailed analysis of the toy datasets and highlights the close approximation of intrinsic dimensions for $\mathbb R^d$ surfaces.
MNIST
Let’s try to see TwoNN in action and compute the intrinsic dimension of an image dataset (MNIST). The blue bars in the figure below represent the predicted intrinsic dimensions for various digits in the dataset. The intrinsic dimension of the digit 2 in the dataset is estimated to be around $14.5$. Let’s see if adding extra information like color in MNIST adds to the estimated intrinsic dimensions. For this setup, we use a colored set of MNIST (coloredMNIST, not to be confused with coloredMNIST). In this setting, we add random colors to all the pixels that are not black and observe the change in intrinsic dimensions. We observe that though the estimation of intrinsic dimensions increases as we add noise in color compared to the relative digits, we still see a similar pattern. An interesting observation here is that as the number of white/gray pixels increases, the intrinsic dimension of the digit increases, i.e., digit 1 has the lowest intrinsic dimension, and digit 8 has the highest intrinsic dimension. This pattern is more visible in the colored version of the MNIST dataset.
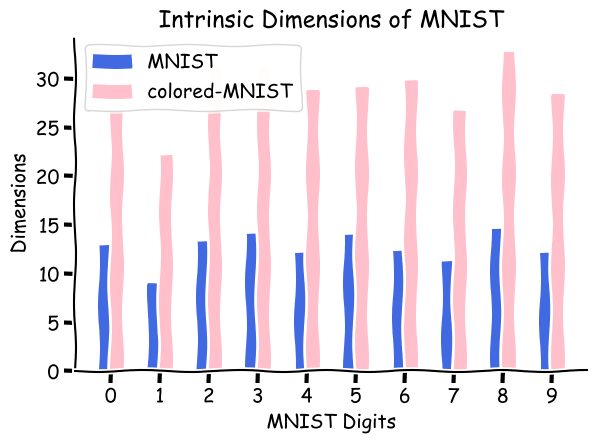
A noteworthy point about the intrinsic dimensions is that the variables used to explain the data here are concerned with the original dimensions of the data points rather than the abstract information compression that humans perform. So when we started thinking about the reason for MNIST’s estimated ID turning out to be around ~14.something, we should have thought in the data space rather than the semantic space. Originally, there lies a pattern in MNIST images, which are believed to be coming from a low dimensional manifold, and the intrinsic dimension of this manifold is ~14.something (approximated according to TwoNN), meaning that the MNIST style images can be compressed to ~15 dimensions without losing any information. So, the computation of intrinsic dimension has nothing to do with the number of digits present in the dataset, but it instead is the number of dimensions required to explain the dataset in its original space.
Sneak Peak to GRIDE
A recent work on similar lines (Denti et al., 2022) presents a generalized version of the TwoNN algorithm and provides a more robust way of computing intrinsic dimensions. Instead of taking $R = {r_2\over r_1}$, i.e., the ratio of distance using the first and the second nearest neighbors, GRIDE suggests considering the $k^{th}$ and the $l^{th}$ nearest neighbors to estimate the intrinsic dimension and formulates the following closed-form expression for the probability distribution.
$$ \begin{gathered} \mu_{i,k,l} = {r_{i,k}\over r_{i,l}} \\ p(\mu_{i,k,l} = \mu_0) = \begin{cases}\displaystyle{d (\mu_0^d -1)^{k-l-1} \over \mu_0^{(k-1)d + 1}B(k-l, l)} & \mu_0 > 1 \\ 0 & \text{otherwise} \end{cases} \end{gathered} $$
where $B(\cdot, \cdot)$ is the beta function. The below figure shows how the probability estimates change as we change the value of $k$ and $l$.
Further, using the above probability distribution, they propose an optimization problem over the variable $d$ to estimate the intrinsic dimension.
$$ \log \mathcal{L}(d)=N \log d+\left(k_2-k_1-1\right) \sum_{i=1}^N \log \left(\mu_i^d-1\right) \qquad \qquad \qquad \qquad \\ \qquad \qquad \qquad \qquad \qquad -\log \left(B\left(k_2-k_1, k_1\right)\right) \ -\left(\left(k_2-1\right) d+1\right) \sum_{i=1}^N \log \left(\mu_i\right) $$
which is a concave optimization problem and can be solved using standard concave optimizers. We tried exploring if we can solve the above optimization problem using CVXPY library; however, in the optimization problem above, the objective function relies on the parameter which of the form $\mathcal{O}(\mu^{d})$ (not implemented in the current version of the library as of December 2023).
Conclusion
In this post, we went through the underlying perspective of the Poisson process that TwoNN provides for computing intrinsic dimensions. We also went through the math behind the computation of intrinsic dimensions and how it can be approximated using the ratio of the two nearest neighbors. Further, we sneak peeked into the GRIDE algorithm, which also provides a generalization of the twoNN algorithm. We performed some experiments to see the effect of adding additional information to the dataset and how it affects the intrinsic dimensions. Overall, we hope this post provides a good starting point for anyone who wants to explore the field of intrinsic dimensions.